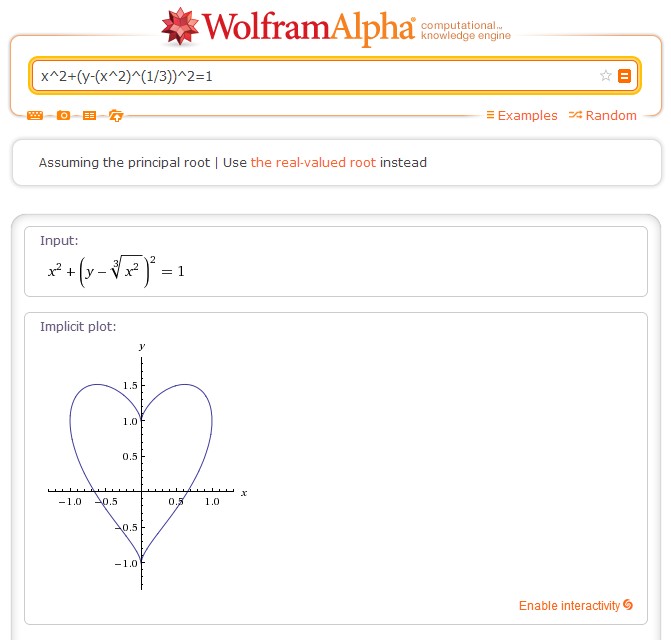
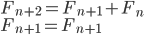|
1 2 3 4 5 6 7 8 9 10 11 |
#-*- coding:utf-8 -*- from collections import Counter # 统计总汉字数,文本均以utf-8格式保存 TotalChar = [x for x in open("D:\Eric5\红楼梦.txt", "r", encoding="utf-8").read() if 19968<=ord(x)<=40869] # 统计不同汉字的重复次数 CountChar = Counter(TotalChar) print("总汉字数:", len((TotalChar))) print("不同汉字数:", len((CountChar))) print(CountChar) |
对我国四大名著的统计结果如下,并列出重复次数最多的前十个字:
《红楼梦》
总汉字数: 731598
不同汉字数: 4253
[('了', 21229), ('的', 15736), ('不', 15038), ('一', 12194), ('来', 11450), ('道', 11061), ('人', 10558), ('是', 10151), ('说', 9710), ('我', 9176)]
《西游记》
总汉字数: 584058
不同汉字数: 4458
[('道', 10994), ('不', 8827), ('一', 7910), ('了', 7690), ('那', 7494), ('我', 7138), ('是', 6463), ('来', 5935), ('他', 5729), ('个', 5683)]
《水浒传》
总汉字数: 705654
不同汉字数: 4074
[('了', 11459), ('道', 10433), ('一', 10029), ('来', 97[......]
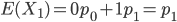

 [......]
[......]

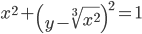

 [......]
[......]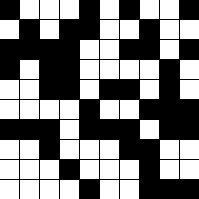 其中黑色的小格子有45个,白色的小格子有55个,则按照上述所说的迭代规则,最后所有格子变成黑色的概率为45/100,而所有格子变成白色的概率为55/100。
其中黑色的小格子有45个,白色的小格子有55个,则按照上述所说的迭代规则,最后所有格子变成黑色的概率为45/100,而所有格子变成白色的概率为55/100。