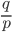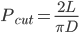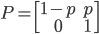Random Walk in VAR
贝特朗悖论：在一给定圆内所有的弦中任选一条弦，求该弦的长度长于圆的内接正三角形边长的概率。
至少有三种方法可以在一个圆上随机选择一条弦，如下：
解法一：如左图，由于对称性，可预先固定弦的一端。仅当弦与过此端点的切线的交角在60°～120°之间，其长才合乎要求。所有方向是等可能的，则所求概率为1/3。此时假定端点在圆周上均匀分布。
解法二：如中图，由于对称性，可预先指定弦的方向。作垂直于此方向的直径，只有交直径于1/4点与3/4点间的弦，其长才大于内接正三角形边长。所有交点是等可能的，则所求概率为1/2。此时假定弦的中心在直径上均匀分布。
解法三：如右图，弦被其中点位置唯一确定。只有[......]
蒙提霍尔问题，亦称为蒙特霍问题或三门问题（英文：Monty Hall Problem）[1]，是一个源自博弈论的数学游戏问题，大致出自美国的电视游戏节目Let's Make a Deal。问题的名字来自该节目的主持人蒙提·霍尔（Monty Hall）。
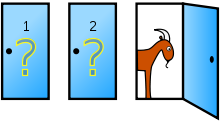这个游戏的玩法是：参赛者会看见三扇关闭了的门（X、Y、Z），其中一扇的后面有一辆汽车，选中后面有车的那扇门就可以赢得该汽车，而另外两扇门后面则各藏有一只山羊。当参赛者选定了一扇门（例如X），但未去开启它的时候，知道门后情形的节目主持人会开启剩下两扇门的其中一扇（例如Y），露出其中一只山羊。主持人其后会问参赛者是坚持原来的选择（即X）呢，还[......]
一个赌徒在每次赌博中以概率p赢一个单位，并以概率q=1-p输一个单位，假设各次赌博都是独立的，赌徒在开始时有a个单位，问他的财富在达到0（即破产）前先达到N的概率是多少[1]？
设Pa(a=0,1,…,N)记赌徒在开始时有a个单位而且他的财富最终达到N的概率。通过对初始的一次赌博的结果取条件，我们得到
由于p+q=1，上式等价地有
或者
(Pa - Pa-1), a=1,2,…,N-1由于P0[......]
以下的第一个匹配问题摘自[1]：
问题：假如你有一个装了n个无差别的球的罐子，每个球分别贴了1,2,3,…,n的标签。每次取出一个球直至所有球均取出，那么，至少有1个球的取出顺序与它的标签一致的概率是多少（例如，标签为2的球是第2个取出来的）？
解答 n个球有n!种排列顺序，假设在某一排列中第j个元素代表第j个取出的球。令Pj(j=1,2,…,n)代表某一给定的排列的第j个取出的球的标签为j，并且令Aj代表具有属性Pj的排列的集合。那么，至少有1个球的取出顺序与它的标签一致的排列的数量Ln为
$$! \begin{array}{l} {{L}_{n}}=|{{A}_{1}}\cup {{[......]
连续抛掷一枚标准的骰子（即出现6种点数的概率一样，均为1/6）直至点数和超过12。则点数和最有可能是多少？例如，如果点数依次为3、6、1、5，则点数和为15。
解 一种解法是穷举所有点数系列，看看哪个点数和最有可能。但有另一种更巧妙的方法。假如点数系列之和为14，则最后一次抛骰子的点数不可能是1，否则点数和为13（已经超过12）而终止。对于产生14的所有点数系列，如果最后一次的点数均减少1，则可以产生13（因得到14的最后一次不能是1，所以得到14的最后一次骰子点数只能是2、3、4、5、6，那么若最后一次骰子点数改为1，2，3，4，5，这些点数系列之和就会得到13），因此，出现点数和为[......]
浦丰投针问题（Buffon’s Needle Problem）是几何概率的经典问题之一，由George-Louis Leclerc和Comte de Buffon于1777年提出——平面上画有等距离为D（D>0）的无限多条平行线，向此平面投掷一根长度为L（L≤D）的针，则该针与任一平行线相交的概率Pcut为：
在数轴上的区间[0 1]上有两个随机点A和B，它们的坐标服从[0 1]上的均匀分布，即X1~U(0,1)，X2~U(0,1)。则此两点间距离的数学期望是多少？
两点间的距离X = |X1-X2| = max{X1,X2} - min{X1,X2}。令Y = max{X1,X2}， Z = min{X1,X2}，两者的累积分布函数为：
F(Y) = P(Y≦y) = P(X1≦y & X2≦y) = P(X1≦y) × P(X2≦y) = y×y = y2
F(Z) = P(Z≦z) = 1-P(Z≧z) = 1-P(X1≧z & X2≧z) = 1 - P(X1≧z) × P(X[......]
Collecting Coupons: Coupons in cereal boxes are numbered 1 to 5, and a set of one of each is required for a prize. With one coupon per box, how many boxes on the average are required to make a complete set?
这是《Fifty Challenging Problems in Probability with Solutions》书中的第14个题目[1]。在第一个盒子中，我们得到其中一个数字[......]
生日问题[1-2]是指在随机选择的一群人当中有两人的生日相同的概率。如果一个房间里有23个或23个以上的人，那么至少有两个人的生日相同的概率要大于50%；对于60或者更多的人，这种概率要大于99%。计算与此相关的概率被称为生日问题，在这个问题之后的数学理论已被用于设计著名的密码攻击方法：生日攻击。
假设有n个人在同一房间内，不考虑特殊因素，例如闰年、双胞胎，并且假设一年365日出生概率是均匀分布的。首先计算每个人的生日日期都不同的概率为：
$$!\begin{equation} \overline{p(n,365)}=\frac{A_{365}^{n}}{{{365}^{n}}} \en[......]
