单位区间[0 1]里随机分布n个点

在数轴上的区间[0 1]上有两个随机点A和B，它们的坐标服从[0 1]上的均匀分布，即X₁~U(0,1)，X₂~U(0,1)。则此两点间距离的数学期望是多少？

两点间的距离X = |X₁-X₂| = max{X₁,X₂} - min{X₁,X₂}。令Y = max{X₁,X₂}， Z = min{X₁,X₂}，两者的累积分布函数为：

F(Y) = P(Y≦y) = P(X₁≦y & X₂≦y) = P(X₁≦y) × P(X₂≦y) = y×y = y²

F(Z) = P(Z≦z) = 1-P(Z≧z) = 1-P(X₁≧z & X₂≧z) = 1 - P(X₁≧z) × P(X₂≧z)
= 1 - (1-z)×(1-z) = 1-(1-z)²

两点坐标值的最大值与最小值的概率密度函数分别为：

f(Y) = F^'(Y) = 2y ， f(Z) = F^'(Z) = 2(1-z)

则两点坐标值的最大值与最小值的数学期望分别为：

E(Y) = 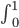yf(Y)dy = 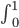2y²dy = 2/3
E(Z) = 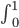zf(Z)dz = 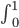2z(1-z)dz = 1/3

所以两点间距离的数学期望 E(X) = E(Y) - E(Z) = 2/3 - 1/3 = 1/3

在数轴上的区间[0 1]上随机分布的n个点，它们的坐标服从[0 1]上的均匀分布，即X₁~U(0,1)，X₂~U(0,1) ，…，X_n~U(0,1)。则相距最远的两点间的距离的数学期望是多少？

此例是上一例的推广。令Y = max{X₁,X₂,...,X_n}， Z = min{X₁,X₂,...,X_n}，则有：

F(Y) = yⁿ ， F(Z) = 1-(1-z)ⁿ

n个点中坐标值的最大值与最小值的概率密度函数分别为：

f(Y) = F^'(Y) = ny^n-1 ， f(Z) = F^'(Z) = n(1-z)^n-1

则n个点坐标值的最大值与最小值的数学期望分别为：

E(Y) = 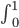yf(Y)dy = 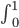nyⁿdy =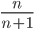
E(Z) = 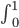zf(Z)dz = 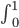zn(1-z)^n-1dz =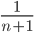

所以相距最远的两点间距离的数学期望 E(X) = E(Y) - E(Z) = =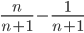

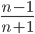
在数轴上的区间[0 1]上随机分布的n个点，它们的坐标服从[0 1]上的均匀分布，即X₁~U(0,1)，X₂~U(0,1)，…，X_n~U(0,1)。n个点把区间[0 1]分成n+1段，每段长分别为L₁，L₂，…，L_n。求L_i(i=1,2,…,n)的数学期望？

对于第一段L₁，由第二例可知：E(L₁) = 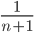。求第一段长的数学期望的另一种方法如下：

由于X₁是最左的一个点，令L₁长为t，则每个点坐标值都大于等于t，有：
P(X₁≧t) = (1-t)ⁿ

所以P(X₁≦t) = 1-(1-t)ⁿ， f(L₁) = P^'(X₁≦t) = n(1-t)^n-1

E(L₁) = 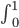tn(1-t)^n-1dt =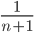

对于第二段L₂长度的数学期望，可等价为在区间[0 (1-X₁)]里随机分布n-1个点时第一段的长度的数学期望，即为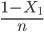的期望值。所以：

E(L₂) = = =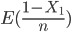

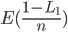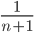
以此类推可得，n个点把区间[0 1]分成n+1段，每段长度的期望值均为。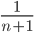

《Fifty Challenging Problems in Probability with Solutions》^[1]书中的第38个题目讨论了以上的第三个例子，并给出如下定理：

对称定理：当n个点随机掉落于某区间，则分割出的n+1个小区间的长度具有相同的分布。

The First Ace Shuffle an ordinary deck of 52 playing cards containing four aces. Then turn up cards from the top until the first ace appears. On the average, how many cards are required to produce the first ace?

这是《Fifty Challenging Problems in Probability with Solutions》^[1]书中的第40题。4张A牌把剩余的48张牌分成5堆，每堆张数为0~48。如果两张A牌前后排列着，则它们之间的牌数就是为0。根据上面第三个例子的结论，5堆牌平均每堆有48/5=9.6张牌，所以要翻到第一张A牌，则平均需要翻9.6+1=10.6张牌。