斐波那契数列[1]指的是这样一个数列:0、1、1、2、3、5、8、13、21……,每一项是其前面两项之和,即有通式:F0=0,F1=1,F2=1,Fn+2=Fn+1+Fn(n∈非负整数)。
下面通过线性代数的方法来求得斐波那契数列的通式Fn。
令 ,则
,则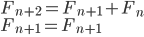 可表示为
可表示为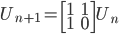 ,因此,
,因此,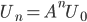 。若λ1是矩阵A的特征根,相应的特征向量为x1,则有
。若λ1是矩阵A的特征根,相应的特征向量为x1,则有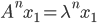 ,因此,若把U0表示成A的特征向量的线性组合,则Un可表示成A的特征向量的线性组合。
,因此,若把U0表示成A的特征向量的线性组合,则Un可表示成A的特征向量的线性组合。
求解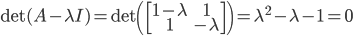 ,可得A的特征根分别为:
,可得A的特征根分别为: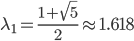 、
、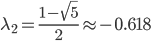 ,相应的特征向量为
,相应的特征向量为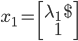 、
、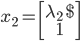 ,则有:
,则有: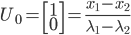 。
。
因此,斐波那契数列第n和n+1项为

第n项为
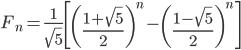
由上面的通式可以看出,当n→∞时,
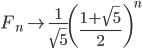 ,相邻两项之比
,相邻两项之比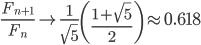 ,即是当n趋向于无穷大时,后一项与前一项的比值越来越逼近黄金分割0.618。
,即是当n趋向于无穷大时,后一项与前一项的比值越来越逼近黄金分割0.618。
以下列举斐波那契数列应用于组合数学的例子:
(1)有一段楼梯有10级台阶,规定每一步只能跨一级或两级,要登上第10级台阶有几种不同的走法?
这就是一个斐波那契数列:登上第一级台阶有一种登法;登上两级台阶,有两种登法;登上三级台阶,有三种登法;登上四级台阶,有五种登法……
1,2,3,5,8,13……所以,登上十级,有89种走法。
(2)类似的,一枚均匀的硬币掷10次,问不连续出现正面的可能情形有多少种?
答案是F12=144种。
(3)求递推数列a1=1,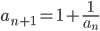 的通项公式?
的通项公式?
由数学归纳法可以得到: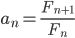 ,将斐波那契数列的通项式代入,化简就得结果。
,将斐波那契数列的通项式代入,化简就得结果。
参考:
[1] http://baike.baidu.com/view/816.htm
[2] Gilbert Strang. Introduction to Linear Algebra, 4th edition.
[1] http://baike.baidu.com/view/816.htm
[2] Gilbert Strang. Introduction to Linear Algebra, 4th edition.
Speak Your Mind