Stepping Stone Model

[1]中第11章有个例子介绍了应用于遗传学的“Stepping Stone Model”（中文似乎翻译为踏脚石模型）。在该模型中，有N×N个小格子组成的方阵，初始时每个小格子从k种颜色中等概率地随机选择一种颜色。在每一次迭代中，这N×N个小格子中的一个被随机挑选到，它的颜色等概率地变为围绕它的8个小格子中的一个，为了避免边界问题，认为在方阵最左边上的小格子是与最右边的小格子相邻，最上边的小格子与最下边的小格子相邻。经过足够多次的迭代后，最终所有格子都会变成同一种颜色，而这k种颜色最后能胜出的概率等于初始时该颜色的小格子的数目占总数（N×N）的比例。

举一个简单的例子，当N=10，k=2（黑、白）时，如果初始时这100个小格子的颜色如下图所示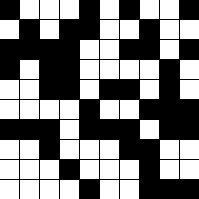：其中黑色的小格子有45个，白色的小格子有55个，则按照上述所说的迭代规则，最后所有格子变成黑色的概率为45/100，而所有格子变成白色的概率为55/100。

考虑赌徒破产问题，当赌徒初始有a单位财富，在每一次赌博中，他以1/2概率输掉1单位财富，以1/2概率赢得1单位财富，则他最后能赢得N单位财富的概率为a/N。以另一种角度考虑这个问题，假设进行了n次赌博后，赌徒有K_n单位财富，则再进行一次赌博后，他的财富期望值为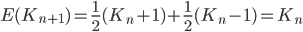，即下一次赌博后的财富期望值等于目前的财富，这种性质在概率论中叫做鞅^[2]。那么，当赌徒初始有a单位财富时，他进行了一次赌博后，他的财富期望值仍为a，如此进行了多次，直到赌徒破产（财富为0）或者财富增加到N单位，这一过程中赌徒的财富期望值一直是a，则令p为赌徒的财富能够达到N的概率，q为赌徒破产的概率，那么必定有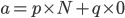：，从而推出。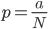

回到踏脚石模型，N×N个小格子从k中颜色中初始化，考虑一次对所有格子进行迭代（即迭代N²次），则每个格子的颜色期望值将含有它周围的8个格子颜色的各自1/8，当把所有格子颜色进行统计时，8份1/8颜色恰好能拼凑起1份颜色，也就是说，这种迭代N²次的方式，将不会改变每个格子的颜色数目的多少。因此，当某种颜色初始时有a个格子，假设这种颜色最后胜出的概率为p，则有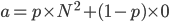，得到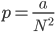，即为初始时该颜色所占比例。也就是说，这N²个格子最后全变为某一种颜色的概率等于该颜色在初始时所占比例。