一个具有n个状态的马尔可夫链如果存在正整数N,使从任意状态i经过N次转移都能以大于零的概率到达状态j(i,j=1,2,...n),则称此马氏链为正则链(Regular Markov Chains)[1]。
正则链的判断方法:对于概率矩阵P,若其某幂次方Pm的所有元素皆为正数,则矩阵P称为正规概率矩阵,此时马氏链称为正则链,或者称马氏链具有遍历性(Ergodicity)[2]。
一个具有遍历性的马尔可夫链经过相当长的时间后,它处于各个状态的概率趋于稳定,且概率稳定值与初始状态无关。在工程技术中,当马尔可夫链的极限概率分布存在时,它的遍历性表示一个系统经过相当长时间后趋于平衡状态,这时,系统处于各个状态的概率分布既不依赖于初始状态,也不再随时间的推移而改变。
正则链的极限分布 是方程组
是方程组

的唯一解。
正则链具有两个重要的描述性参数:平均首次经过时间(Mean First Passage Time)和平均返回时间(Mean Recurrence Time)。
定义:如果正则链刚开始处于状态si,那它第一次到达状态sj的平均转移次数称为平均首次经过时间(Mean First Passage Time),记为mij,且mii=0。
需要计算正则链从其它状态到达状态sj的平均转移次数时,可以令状态sj为吸收状态,从而把正则链转换为吸收链,再根据吸收链性质计算正则链平均首次经过时间,如下例子所示。
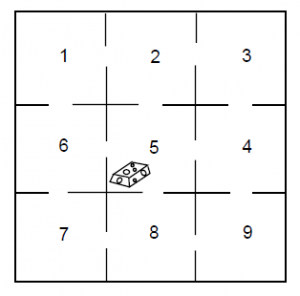
老鼠在这迷宫中觅食,一旦它到达格子5,就停下来享受食物,标准形式的转移矩阵如下所示:

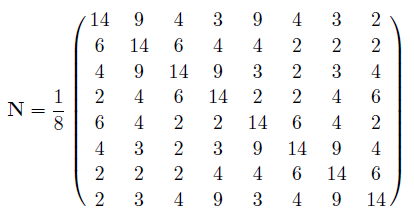
基本矩阵N为:
从其它状态到达状态5(吸收状态)的平均时间由Nc给出:
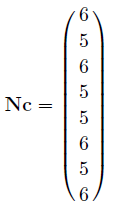
从结果可以看出,若从格子1出发,则老鼠平均需要6步找到食物,由对称性可知,若从格子3、7或者9出发,平均步数也是一样的,这比从2、4、6或者8出发要多花费1步。
定义:如果正则链刚开始处于状态si,那它第一次返回状态si的平均转移次数称为状态si的平均返回时间(Mean Recurrence Time),记为ri。
正则链状态si的平均返回时间为ri=1/πi,其中πi是正则链的极限分布π=(π1,π2,...)的第i个元素。
正则链的基本矩阵定义为:
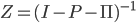
其中,当n→∞时,Pn→

正则链的平均首次经过时间矩阵M由其基本矩阵Z和极限分布π决定:
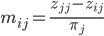
[1] Chapter 11, Introduction to Probability, http://goo.gl/gjfsd
[2] http://en.wikipedia.org/wiki/Ergodicity
[...] 正则链的极限分布pi =({{pi }_{1}},{{pi }_{2}},cdots )是方程组 [...]